Lineární programování
Úloha lin. programování - optimalizovat hodnotu LINEÁRNÍ účelové funkce,
přes prostor možných řešení, vymezený LINEÁRNÍMI podmínkami
Lin. účelová fce - max c1x1 + c2x2 + ...
+ cnxn, kde x1, ... xn jsou proměnné a c1, ... cn
konstanty.
Lineární podmínky -
a11x1 + an2x2+ ... + a1nxn ≤ b1
... ...
an1x1 + an2x2+ ... + annxn ≤ bm
b
i - konstanta
∈ R,
∀i
∈<1,m>
a
ij - konstanty
∈ R,
∀i
∈<1,m>,
∀j
∈<1,n>
Úloha ve standardním tvaru zní: Nalezněte vektor x∈R, jež maximalizuje
účelovou funkci cTx za podmínek Ax ≤ b, kde c∈R, b∈Rn, A∈Rmxn.
Přípustné řešení - každý vektor x, jež splňuje Ax ≤ b.
Optimální řešení - takové přípustné x*, že pro
každé přípustné x platí, že cTx ≤ cTx*
Geometrická interpretace
1 podmínka určuje poloprostor Rn. Všechny podmínky dohromady odpovídají průniku těchto poloprostorů -
označuje se jako simplex (může být omezený i neomezený). Účelová funkce udává roviny se stejnou
normálou, tato normála určuje gradient(směr), ve kterém se snažíme maximalizovat/minimalizovat.
K oboru hodnot
Budeme uvažovat jen R. C, Zn nepřicházejí v úvahu - nejsou uspořádané. Řešení pouze v Q - platí
úplně stejné postupy. Uvažuje se též obor Z (i když není těleso) - dostaneme úlohy celočíselného
programování(ILP) - na rozdíl od normálního LP těžké. Ze simplexu by celá čísla vybrala jen mřížové
body, optimum které dává simplex v R nemusí být mřížový bod, a nejbližší mříž. bod může být daleko; dokonce
nemusí existovat.
Pomocí ILP lze formulovat úlohu nalezení největší nezávislé množiny v grafu G:=(V,E) - takové
množiny vrcholů, kde žádné dva nejsou spojeny hranou. Za každý vrchol - proměnná xi, hodnota xi
- 0 ≤ xi ≤ 1, za každou hranu (i,j) dám podmínku, že xi +
xj ≤ 1. Optimální řešení - celočíselný vektor. Proměnné, které jsou označeny jedničkou, jsou v
max. nezávislé množině.
Protože nalezení max. nezávislé množiny grafu je NP-úplná (těžká) úloha, je ILP také NP-úplná.
(Neexistuje pro ni polynomiální algoritmus - narozdíl od LP.)
Jaká mohou být řešení úloh LP?
úloha nemá řešení, protože nemá přípustné řešení. Např: x1,x2 ≥ 10,
x1 + x2 ≤ 19. (už ani nezávisí na účel. fci c)
Úloha nemá řešení, protože hodnota účelové fce je neomezená. => není optimální řešení.
Např. x1,x2 ≥ 0, -1 ≤x1 - x2 ≤ 1, max x1 +
x2. To že simplex je neomezený, neznamená automaticky, že optimální řešení neexistuje - viz min.
x1 + x2.
Optimum je jednoznačné.
Úloha má ∞ optimálních řešení. Např - 0 ≤ x1, x2 ≤ 2,
x1 + x2 ≤ 3, max x1+x2. Optimum - úsečka.
Vektor c
∈R
n, matice A
∈R
mxn, b
∈R
m. Hledáme
x
∈R
n, tak, že Ax ≤ b & c
Tx je maximální. Geometricky:
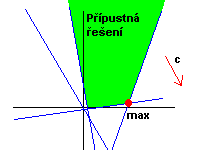
a
ix ≤ b
i ... přímky. Přípustné řešení splňuje všechny nerovnosti.
Pro minimum cTx - hledáme max. -cTx
Chceme-li a11x1 + .... + a1nxn ≥ b1,
potom přepíšeme: -a11x1 - .... -a1nxn ≤ -b1
Chceme-li rovnost aiTx = bi, nahradíme dvěma nerovnostmi,
aiTx ≤ bi; aiTx ≥ bi.
Chceme-li dostat a11x1 + ... + a1nxn ≤ b1
v matici, kde Ax = b, uvažujeme a11x1+ ... + a1nxn + xn+1 =
b1, kde xn+1 ≥ 0 (- přidáme jednu proměnnou navíc).
Chceme-li pracovat s nezápornými proměnnými: místo xi zavedeme 2 proměnné x'i
a x"i, ve tvaru x'i - x"i - i záporná čísla jdou napsat jako rozdíl 2 kladných
čísel.
Množina V ⊆ Rn je konvexní, pokud ∀u,v ∈ V
platí, že {αu + (1 - α)v; α ∈<0,1>} ⊆ V (spojnice u,v je též podmnožinou V).
Průnik dvou konvexních množin je zase konvexní množina. (V1,V2 konvexní,
u,v ∈ V1 ∪ V2 => {αu + (1 - α)v; α ∈<0,1>}
⊆ V1 ∪ V2).
Množina přípustných řešení je konvexní množina. ( Jeden řádek matice Ax ≤ b - poloprostor,
celé řešení - průnik konečně mnoha poloprostorů (konvexních množin)).
Množina optimálních řešení Ax ≤ b & max. cTx je konvexní množina.
Důkaz: x*, x** ... 2 opt. řešení => cTx* = cTx**,
vezmu α∈ <0,1>, uvážím α(x*) + (1 - α)x** = x'. x' - je přípustné (konv. množina řešení),
cTx' ?= cTx* ... cTx' = αcTx* + (1 - α)cTx**.
Víme, že cTx* = cTx**, z toho: cTx' = cTx*.
Konvexní obal K(X) množiny x ⊆ Rn je průnik všech konvexních
množin v Rn, obsahujících X, tj. K(X) = ∪X⊆VV (konvexní).
v ∈ Rn je konvexní kombinací vektorů u1 ...
un ∈ Rn, pokud existují α1 ... αn ∈ <0,1>,
a navíc ∑ki=1αi = 1, t.ž. v =
∑ki=1αiui.
Věta: Konvexní obal množiny X ⊆ Rn je množina všech konvexních
kombinací prvků z množiny X, tj. K(X) = {u; ex. x1...xk ∈X, α1
... αk, t.ž. u = ∑ki=1αixi,
∑αi = 1, αi ∈ <0,1> }.
(Konvexní) mnohostěn je průnik konečně mnoha poloprostorů v Rn
(polyedr).
Dimenze mnohostěnu P je dimenze nejmenšího (nejméně dimenzionálního)
afinního prostoru, obsahujícího P.
To samé jako dimenze nejmenšího vekt. prostoru obsahujícího P', což je P posunuté do počátku.
Hranice poloprostorů vymezujících P jsou tzv. hraniční nadroviny.
Pokud se n hraničních nadrovin P protíná v právě 1 bodě X, a navíc X∈P, tak bod x
se nazývá vrchol mnohostěnu P
Mnohostěny jsou totéž co množiny přípustných řešení úloh LP. X je vrchol mnohostěnu určeného
Ax ≤ b => podmatice A složená z řádků odpovídajících hraničním nadrovinám určujícím x je regulární.
Počet vrcholů mnohostěnu je nejvýše (nm) - tj. tento
počet je konečný. (Průnik n nadrovin, vybírám z m nadrovin.)
Lemma: Má-li matice A úlohy LP s n proměnnými hodnost n, pak mnohostěn
příslušný k řešení obsahuje vrchol.
Důkaz:Sporem: vezmeme přípustné řešení x
∈P takové, že x leží na
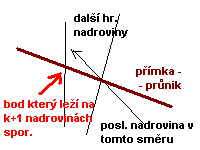
největším možném počtu nezávislých hraničních nadrovin. Tento počet := k. 2 případy:
a) k = n → x je vrchol, spor.
b) k < n.
Průnik vybraných < n nadrovin má
dimenzi ≥ 1 → obsahuje přímku. BÚNO x leží na k prvních nadrovinách. Víme, že A má hodnost n =>
další nadroviny musí průnik k prvních protínat → uvážíme průnik, dostaneme x'
∈(k+1) hr. nadr.,
což je spor.
Věta: Každý omezený KONVEXNÍ mnohostěn je konvexním obalem množiny svých
vrcholů.
Omezený - všechny body mají omezenou vzdálenost od počátku (nebo od sebe navzájem), nebo -
lze ho vnořit do dostatečně velké koule (v Rn - sféry), nebo - neobsahuje polopřímku.
Důkaz: P - mnohostěn, X množina vrcholů P, předp. P ⊆Rn,
X⊆P & P konvexní => K(X) ⊆ P ← K(X) je průnik všech konv. množin, které danou množinu
obsahují. Opačně P ⊆ K(X) - sporem: vezmu x ∈ P \ K(X) takové, že náleží největšímu počtu (=k)
nezávislých hraničních nadrovin.
Když k=n - X vrchol => x ∈ X ⊆ K(X), spor.
k < n - x v nejvíce hr. nadrovinách - průnik těchto k nadrovin musí obsahovat polopřímku (Kdyby ne,
tak x není na nejvíce hr. nadrovinách - x není vrchol) => spor s omezeností.
Věta: Má-li úloha LP optimální řešení a matice této úlohy má hodnost
n rovnou počtu proměnných, potom se potima nabývá též v některém z vrcholů mnohostěnu přípustných
řešení.
Důkaz: Ozn. x* optimální řešení, rank(A) = n, z lemmatu - P má nějaké
vrcholy.
a) P je omezený: x* = ∑ aiui, kde ∑ai = 1, αi
∈ <0,1>, ui jsou vrcholy P. Potom jakmile a1≠0, musí platit, že cTx*
= cTui. Obecně platí, cTx* ≤ cTui, protože cTx*
= ∑αicTui →když bych hodnotu snížil, bude mi chybět (∑αi
= 1) - celk. hodnota je menší) => cTx* = cTui. Potom ui je
vrchol, kde se nabývá optima.
b) pokud je P neomezený, x* leží určitě na hranici P (protože nadrovina určená rovnicí cTx = cTx*
protíná hranici polytopu (jinak by nebylo def. optimální řešení) - celý P leží na 1 straně nadroviny). Nechť x* leží
v h nezávislých hraničních nadrovinách. Označmě B průnik těchto nadrovin. Hodnota účelové funkce cTx musí
být konstantní na množině B (kdyby ex. y, y' ∈ B : cTy > cTy', potom pro dostatečně
malé ε platí, že x* + ε(y - y') ∈ B ∪ P. Potom cT(x*+ε(y - y')) =
cTx* + ε(cTy - cTy') → nejde, x* je optimum.).
Vrcholy B ∪ P jsou vrcholy P ... průniky některých nadrovin určujících P. Vezmu některý z nich, nabývá se
tam optima (musí existovat, protože hodnost matice určující B ∪ P je n (B & P pod sebou v matici)).
Simplexový algoritmus/metoda
- Postup jak vyřešit úlohu LP procházením množiny vrcholů mnohostěnu přípustných
řešení tak, že hodnota účelové funkce neklesá
- Pozor, může trvat exponenciálně dlouho vzhledem k dimenzi/počtu rovnic - hyperkrychle v Rn určená
2n nadrovinami má 2nvrcholů
- V průměrném případě v polynomiálním čase.
- V praxi se nepoužívá, existují rychlejší metody.
Příprava tvaru úlohy pro LP.
Standartní tvar: max cTx, Ax ≤ b.
Výchozí tvar - max cTx pro simplex Ax = b,
x ≥ 0 (! není stejná matice jako v předch. !) - A → ( A | I ).
Když b ≥ 0, víme, že existuje přípustné výchozí řešení, t.ž. pomocným proměnným dosadím
hodnoty z b.
Lemma: Nechť max cTx, Ax = b, x ≥ 0 je úloha L.P. (Předp., že
c ∈ Rn, b ∈ Rm, A ∈ Rmxn a rank(A) = m (m ≤ n). Nechť
B ⊆ {1,2,..,n}, |B| = m je množina indexů taková, že čtvercová matice AB je regulární. Potom
existuje jedné přípustné řešení této úlohy LP, t.ž. xi = 0 ∀ i ∉ B.
Důkaz: Ostatní proměnné xi, i ∈ B jsou určeny soustavou
ABx = B, což je soustava s regulární maticí => je to jednoznačné (← příp. řešení, protože
je i přípustné řešení Ax = b, ost., nulové proměnné řešení neovlivní.
Řešení z předch. lemmatu se nazývá bázické přípustné řešení úlohy LP,
určené bází B.
Báze B je báze úlohy LP, což nesouvisí s bází vekt. prostoru.
Proměnné xi, x ∈B se nazývají bázické, ostatní jsou
nebázické.
Příklad:
max(x1 + 2 x2)
x1 - x2 ≤ 2
-x1 + x2 ≤ 1
2x1 + x2 ≤ 7
x1, x2 ≥ 0.
→
→
→
→
→
→
max(x1 + 2 x2)
x1 - x2 + x3 = 2
-x1 + x2 + x4 = 1
2x1 + x2 + x5 = 7
x1, ..., x5 ≥ 0.
(přepis matice). x
3, x
4, x
5 - pomocné proměnné. Poč.stav:
------------------------
x3 = -x1 + x2 + 2
x4 = x1 - x2 + 1
x5 = -2x1 - x2 + 7
-------------------------
Vektor b = (2,1,7) určuje hodnoty bázických proměnných.
Účelová fce z = x1 + 2x2 ( = 0 )
B := {3,4,5}
Pokusíme se zvýšit z ... zvýším např. x
1 - provedu substituci:
------------------------
x1 = -x3 + x2 + 2
x4 = - x3 + 3
x5 = 2x3 - 3x2 + 3
-------------------------
z = -x3 + 3x2 + 2 = 2
(Množina přípustných řešení zůstává stejná)
→ zvednul jsem hodnotu účel. fce.
Postupně: rozhodnu se, kterou proměnnou mohu zvýšit, aby se zvýšila hodnota účelové fce a zvednu ji.
Přepíšu, přesunu se - post. do dalších vrcholů až najdu maximum.
Důsledek: Báze B určuje bázické přípustné řešení <=>
AB-1b ≥ 0.
Důkaz: x je řešením Ax = b. AB-1Ax
= AB-1b, AB-1A ... AB-1AB = I,
xi = AB-1b, i ∈ B (nezáporný, pokud AB-1b ≥ 0),
xi = 0 pro i ∉ B (nezáporný vždy).
Pro úlohu lin. prog a přípustnou bázi B definujeme
simplexovou tabulku
následovně:
| |
B | A | b
---+-----+---
|c^T |-z
B - báze, A - podmínky, b - vektor pravých stran
c
T - účelová fce, z - hodnota účel. fce.
, kde matice soustavy A |b je upravena element. úpravami, tak že A
B = I, a podobně poslední řádek
c
T|z je upraven tak, že c
i = 0 pro
∀ i
∈ B.
Pro úlohu:
3 | 1 -1 1 0 0 | 2
4 | -1 1 0 1 0 | 1
5 | 2 1 0 0 1 | 7
--+----------------+--
| 1 2 0 0 0 | 0
{3,4,5} - přípustná báze, protože (x
3|x
4|x
5) dávají dohromady I
n.
účelová fce - u 3, 4, 5 - jenom nuly
Pro jednoduchost budeme indexovat řádky tabulky indexy z množiny B (př. B → b3
= 2). (Levý sloupec tabulky - "B" určuje číslo řádku).
Jak poznat, kolik je hodnota účelové funkce ?
Označíme f(x) hodnotu účelové funkce v bodě x.
-
Při prvním sestavení tabulky dáme do posl. řádku cT|f(x).
- Elementární úpravy nemění platnost
rovnice cTx = f(x) -z, neboli cT | z → c'T | z'.
- Je-li x bázické řešení příslušné bázi B, potom máme cTx = 0, neboli f(x) = z. (maximalizujeme z).
(pro bázické řešení: i∈B - cTi= 0, i∉B xi = 0, proto cTx
= 0; cTx = f(x) - z = 0).
Simplexový algoritmus
0. Nalezni nějaké přípustné řešení a sestav simplexovou tabulku pro tuto přípustnou bázi B. (jde udělat,
viz dále).
Opakuj:
- Jestliže cj ≤ 0 pro ∀j∉B, potom STOP, příslušné bázické řešení je optimální
(nemůžu zvednout žádnou proměnnou), jinak zvol j∈B: cj> 0 (j - pivot). (zapamatuji si, co chci
zvětšit).
- Jestliže akj ≤ 0 pro ∀k ∈B, potom STOP, úloha LP je neomezená (proměnné mohou jít
k ∞, rovnost stále platí). Jinak najdi i ∈B : bi/aij = min{
bk/akj : akj > 0 & k ∈ B } (Zjištuji, kam až mohu proměnnou zvednout,
vyberu si řádek, kde mám nejtěsnější omezení.)
- Polož B:= B ∪ {j} \ {i} a uprav tabulku. (provedu záměnu za řádku, kde mám nejtěsnější omezení)
Příklad - 1 krok simplex. algoritmu:
3 | 1 -1 1 0 0 | 2
4 | -1 1 0 1 0 | 1
5 | 2 1 0 0 1 | 7
--+----------------+--
| 1 2 0 0 0 | 0
- zvolím j=1, protože c
j ≥ 0.
možné záměny - za 3 nebo 5,
protože a
kj > 0.
spočítám minima - i = 3.
Nová tabulka:
1 | 1 -1 1 0 0 | 2
4 | 0 0 1 1 0 | 3
5 | 0 3 -2 0 1 | 3
--+----------------+--
| 0 3 -1 0 0 |-2
- sloupce A 1,4,5 dávají dohromady I
m.
- posl. řádek - ve sloupcích 1,4,5 jsou nuly.
1. řádek - mohu opsat
2. ř. - musím v 1. sl. dostat 0 - sečtu s prvním
3. ř. - odečtu 2x s 1.
to samé pro posledné řádek
dál pokračuje úplně stejně.
Stejný krok jako výše s rovnicemi, jen s tabulkou a čísly.
Obě tabulky odpovídají stejné úloze LP (přesun je pomocí elem. úprav) => množina řešení
se nemění.
Lemma: 3. krok je korektní, neboli: nová báze je přípustná.
Důkaz: Stačí ukázat, že nový vektor b' ≥ 0 (protože A'B
je Im stejně jako AB → A-1Bb ≥ 0, → A-1
Bb' ≥ 0 <=> b'≥ 0).
Pro i: b'i = bi/aij ≥ 0.
(při tvorbě změněné rovnice).
Pro k∈B, k≠i ... b'k = bk - akj
bi/aij ≥ 0 (při elem. úpravách matice) - kvůli volbě i v kroku 2 -
bk/akj ≥ bi/aij.
Lemma: 2. krok je korektní, neboli úloha LP je neomezená, když akj
≤ 0 ∀ B & cj > 0, j ∈ B.
Důkaz: Ozn. x bázické řešení pro danou bázi B. Definuji pomocný vektor y ∈
Rn:
yj = 1,
yk = -akj, k∈B (kladné, protože akj záporné).
yk = 0 jinak.
Potom y ≥ 0 => x + ty ≥ 0 pro t∈(0, ∞). A(x + ty) = Ax + tAy = b (protože Ax=b, Ay=0).
=> libovolný násobek y přičtený k x stále splňuje podmínky.
f(x + ty) = z + tcTy = z + tcj - pro t→∞ jde k ∞. (y má 0 u všech nebázických
proměnných krom j, cT má 0 u všech bázických - zbyde cj).
Lemma: 1. krok je korektní, neboli když c ≤ 0 tak potom je přípustné bázické
řešení x* optimální.
Důkaz: Nechť x je přípustné řešení => x ≥ 0. Potom cTx ≤ 0.
(Protože c≤0).
cTx ≤ 0 = cTx* (je-li bázické řeš. přísl. B, potom cTx = 0).
f(x) = z + cTx ≤ z + cTx* =f(x*)
Pro všechny kroky - 1,2,3 - OK. Zbývá - krok 0 - nevím, jestli mohu dostat přípustné řešení na začátku.
Fakt: Nultý krok lze vyřešit simplexovou metodou na pomocnou úlohu LP.
Důkaz: Původní úloha: max cTx: Ax = b, x ≥ 0. Hledám přípustnou
bázi.
BÚNO předp., že b≥0. (je-li bi < 0, vynásobím řádek -1, změním A, nezměním množinu řešení).
Pomocná úloha: max -y1-...-ym, Ax + Iy = b, x,y ≥ 0.
Výchozí bázické řešení pomocné úlohy: x=0. yi = bi≥0.
Optimum: (existuje vždy, účelová fce je omezena 0):
-y1-...-ym = 0 (y1 = ... = ym = 0 ) - zároveň máme bázické přípustné
řešení původní úlohy: Ax + I⋅0 = b.
Je-li nějaké yi < 0, potom původní úloha nemá žádné
přípustné řešení. (∀přípustné řešení pův. úlohy se dá rozšířit nulami na přpustné řešení pomocné úlohy).
Úloha:
max x1 + x2
------------------------
x1 ≤ 1
x2 ≤ 1
-x1-x2 ≤ -1
x1, x2 ≥ 0
výchozí tvar pro simplex. metodu:
max x1 + x2:
---------------------------------
x1 + x3 = 1
x2 + x4 = 1
x1 + x2 - x5 = 1
x1 ... x5 ≥ 0.
Pomocná úloha:
max -y1-y2-y3:
--------------------------------
x1 + x3 + y1= 1
x2 + x4 + y2= 1
x1 + x2 - x5 + y3= 1
x1 ... x5, y1 ... y3 ≥ 0.
Výchozí pomocné bázické řešení:
x1 ... x5 = 0, y1 ... y3 = 1
Optimum pomocné úlohy:
x1,x4 = 1; x2,x3,x5,y1 ... y3 = 0,
což je výchozí řešení původní úlohy
Konečnost:
Konečnost lze zajistit vhodným výběrem i,j v kroku 1 &2. Pravidlo, které toto dokáže, je tzv.
Blandovo pravidlo (kdykoliv mám více možností, vybírám minimální číslo indexu) => dá se dokázat,
že nikdy nemůžu vybrat dvakrát stejnou bázi - těch je konečný počet => alg. je konečný.
Existují i jiná pravidla výběru i,j (zajišťující lepší výběr) - algoritmus je pak obecně rychlejší, ale
NIKDY nemá polynomiální složitost.
- Metoda "Symbolických perturbací" pro výběr i - mám-li víc možností, trochu pozměním matice
- Elipsoidová metoda - je polynomiálně složitá, v praxi však má tak vysokou konstantu, že se nevyplatí
Dualita lineárního programování
Příklad:mějme úlohu LP:
max x1+ x2:
x1 - x2 ≤ 2
-x1 + x2 ≤ 1
2x1 + x2 ≤ 7
x1,x2 ≥ 0
Otázka: Lze nějak omezit (odhadnout) hodnotu účelové funkce?
např.: (2násobek 3. rovnice: ) 4x1+2x2 ≤ 14 && 4x1 + 2x2
≥ x1 + 2x2 => x1 + 2x2 = cTx ≤ 14 ← odhad.
jinak např.: (sečtení 2. a 3. rovnice:) -x1 + x2 + 2x1 + x2 =
x1 + 2x2 ≤ 8 ← nový horní odhad.
Obecně: Pro úlohu LP:
max cTx = c1x1+ ... + cnxn:
-------------------------------
a11x1 + ... + a1nxn ≤ b1
... ... ...
... ... ...
... ... ...
am1x1 + ... + amnxn ≤ bm
hledáme:
--------
y1
...
...
...
ym
hledáme y
1, ... , y
m, t.ž.
∀ j
∈ {1..n}:
∑
mi=1 a
ijy
i≥c
j
- pokud takové y
1 ... y
m existují, máme horní odhad na hodnotu účelové funkce,
protože:
c
Tx = ∑
nj=1 c
jx
j ≤
∑
nj=1(∑
mi=1a
ijy
i)x
j =
∑
mi=1(∑
nj=1 a
ijx
j)y
i ≤
∑
mi=1b
iy
i = b
Ty.
(protože (∑
mi=1a
ijy
i) ≥ c
j;
(∑
nj=1 a
ijx
j) je vlastně jeden řádek v matici A,
ten ≤ b
i.). - dostal jsem novou úlohu lin. programování.
Pro úlohu LP: max. cTx: Ax≤b, x≥0, tzv. primární úlohu (P) definujeme
duální úlohu (D): min. bTy: ATy ≥ c, y≥ 0.
yi původně odpovídaly řádkům, chci je do sloupců → AT.
k poslední úloze máme duální:
min 2y1 + y2 + 7y3:
-----------------------
y1 - y2 + 2 y3 ≥ 1
-y1 + y2 + y3 ≥ 2
yi ≥ 0.
Duální úlohu lze zformulovat k primární úloze v libovolném tvaru ( sice je
složitější předpis, ale je to možné).
Věta: Nechť úlohy (P) a (D) jsou vzájemně duální úlohy LP. Potom buď
obě úlohy mají přípustná řešení a platí, že cTx* = bTy* pro libovolné optimální x*,
y*, nebo jedna z těchto dvou úloh nemá žádné přípustné řešení a druhá je buď neomezená, nebo také nemá
přípustné řešení.
Příklad: pro úlohu viz výše: 2 optima:
x* = (2, 3)T, y* = (0,1,1)T, cTx* = bTy* = 8.
Důkaz: - založen na korektnosti simplexové metody:
- Simplex. metoda, značení:
Sestavení simplex. tabulky:
tabulku:
| : |
| A : I | b
| : |
-+----------------------+---
| C^T : 0 |
přeznačím jako:
_ .......
A : _ : |
| : A_B : | b
| : : |
-+---_--------_---------+---
| C^T :.c^T_B |
(
cT,
A - celé dohromady)
(
AB,
cTB -
vybrané sloupce
přípustné báze (nemusí být interval).
elementárními úpravami dostanu (na konci simplex. alg.):
| : |
|
AB-1 A
|
AB-1 b =
xB*.
| : |
-+----------------------+---
|
cT -
cTBAB-1A
|
(chci, aby posl. řádek byl ≤ 0 - na konci simplex. alg)
soustavu AB-1 vynásobím zleva AB-1, tím
dostanu Im ve sloupcích určených B. Odečtu od CTB kombinaci řádků z
AB-1 A => dostanu 0.
-
Předp., že (P) i (D) mají přípustné řešení, Potom primární (P) nemůže být neomezená, protože cTx ≤
bTy platí pro lib. dvojici přípustných řešení (viz výše). => (P) není neomezená, má optimální
řešení.
Vezmu x* - nějaké bázické optimální řešení dané bází B. x* je určeno nějakým x*,
což je optimální řešení ve tvaru pro simplexový algoritmus, platí ale, že cTx =
cTx* (cT
je jen doplněním cT pro simplexový algoritmus, víme, že hodnota je stejná). Ze závěrečné
simplexové tabulky plyne:
(x*)i = .... 0 pro i∉B
.... (AB-1b)i
...(v AB je In, toto je bázická část řešení).
Zvolíme y* := (AB-1)T⋅cB a
ukážeme, že y* je optimálním řešením (D).
-
- proč y* je přípustné:
Aby bylo, musí splňovat, že:
ATy ≥ c
y = Imy ≥ 0
ATy ≥ cT
(AT & ImT = Im; cT & 0)
ATy* = AT⋅
(AB-1)T⋅cB
≥ c, protože cT -
cBTAB-1A
≤ 0 na konci simplex. alg. (viz matice výše).
- - proč je y* je optimální:
vyplyne z rovnosti cTx* = bTy* (stačí dokázat toto).
bTy* = bT(AB-1)T cB
= x*B-1 cB =
cBT xB*.
(protože AB-1 b = xB*
na konci simplex. alg. (viz matice); výsledek - číslo mohu transponovat jak chci).
a cBTx*B =
cTx* (protože xi = 0, když i∉B).
- dokázali jsme, že pokud jedna z úloh má optimum, musí ho mít i druhá.
-
2. část věty - triviální, (P) a (D) nemohou být zároveň neomezené, protože by platila první část.
 aix ≤ bi ... přímky. Přípustné řešení splňuje všechny nerovnosti.
aix ≤ bi ... přímky. Přípustné řešení splňuje všechny nerovnosti.
 aix ≤ bi ... přímky. Přípustné řešení splňuje všechny nerovnosti.
aix ≤ bi ... přímky. Přípustné řešení splňuje všechny nerovnosti.
