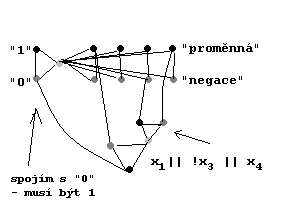
Funguje pro ∀ log. formuli - dá se převést.
g1 || p1 g2 || p2 (obvody-potřeba 2
vv vv dráty na 3 různé stavy)
+-----------------+
| |
+-----------------+
g | | p
v v
DFT:
n-1 n-1 n-1
Aj = ∑ αk eikxj = ∑ αk ei(2π/n)kj = ∑ αk ωkj (O(n2))
k=0 k=0 n=0
Wpq = ωpq, W'pq = ω-pq
n-1 n-1
(W*W')pq = ∑ Wps *W'sq = ∑ ω(p-q)*s
s=0 s=0
p = q - ωi*(p-q) ... = ωi*0 = n.
p ≠ q - Q := ωp-q : Q0 + ... + Qn-1 - geom. řada
- souč.1.n členů - a1(qn - 1)/(q - 1)
Qn-1+1 - 1 1 - 1
∑ Qj = ---------------- * Q0 = --------- * 1 = 0
Q - 1 Q - 1
Qn = ω(p-q)*n = (ωn)(p-q) = 1p-q = 1
n/2-1 n/2-1
Ak = ∑ = a2l ω2lk + ωk ∑ a2l+1 ω2lk
l=0 l=0
n/2-1 n/2-1
Ak+n/2 = ∑ a2l ω2l(k+n/2) + ωk ∑ a2l+1 ω2l(k+n/2)
l=0 l=0
for i = 1 to n do {
while( s nemá následníka = ti && s není kořen )
do s := f( s ); // zpětný odkaz
if ( s má násl. = ti - "s1" ) then s:= s1;
}
B(2) = 1, B(N) = 1 + B( N/2) -> B(N) = log2 N
T(N) = T(N/2) + B(N) = log N + log (N/2) + ...
= k + k-1 + ... = k(k+1) / 2
T(N) = O(1/2 log2 N ).
t: E(G) --> <0,∞), t.ž. ∀ e: 0 ≤ t(e) ≤ c(e),
∀ v ∈ V(G) z ≠ v ≠ s : ∑ t(e) = ∑ t(e)
-->v v-->
t(e) = c(e)
-----------> && δ(v) = 0 v ≠ z => δ(z) = |A|
<-----------
t(e) = 0
dokud ∃ v, v ≠ z, v ≠s : δ(v) > 0 :
vezmi v,
if( ∃ e =(v,w) nebo (w,v) : r(e)>0 (v daném směru) && h(v) ≥ h(w)){
převeď min( δ, r(e)) z v do w
}
else { h(v) := h(v) + 1 }.

/--(expanze)--> [48bit] /---> [32bit- OUT]
[IN- 32bit] | /
xor ---->[48bit]---(8 fcí (6vstupů&4výstupy))
|
[48bit klíč]
[ LINP ] [ RINP ]
| |
xor<---(F)-----+
| | |
v klíč v
[ ROUT ] [ LOUT ]
- 64 bit, 16 iterací (∀ prohodí levý/pravý vstup). Dešifrování - znám vstup do F,
=> mohu si spočítat jeho F, znám i výsl. xor-u => vím i LINP.